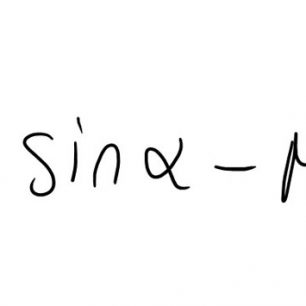Sněhové laviny jsou zkoumány ze všech možných úhlů i pohledů od čistě „uživatelského“ přístupu vhodného pro každého, kdo se pohybuje na tuleních pásech s lyžemi nebo splitboardem. Na volitelný předmět fyzikální seminář FJFI ČVUT Praha v zimním semestru 2020-2021 jsem si připravil vliv lyžaře na možné uvolnění sněhové laviny.
Zprvu jsem přemýšlel, co zvolím za složité teoretické téma, ale pak mě napadlo, že spojím svůj projekt se svou vášní – skialpinismem a horami obecně. A jako první se nabízela fyzika sněhových lavin. Tak jsem začal přemýšlet, co vlastně za tím stojí, pročítal jsem zahraniční články a učil jsem se složité věci. Začal mě tlačit čas před prezentací projektu, tak jsem k tomu začal přistupovat trochu jinak – jen na základě toho, co již vím. Spojil jsem znalosti, co jsem získal na různých kurzech a fyziku, která je probírána v prvním semestru, tedy klasickou mechaniku (Newtonovu). Vymyslel jsem zjednodušený fyzikální model problematiky lavin a došel k poměrně reálným výsledkům.
Newtonovy zákony na sněhu
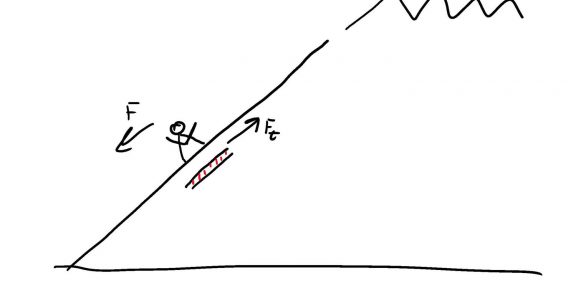
Uvádí se, že přes 90% lavin lidé uvolní sami, vlastní vinou. Je to vcelku i logické z fyzikálního hlediska. Když se člověk pohybuje v lavinovém terénu, tak působí dodatečnou (a často i velkou) silou na sněhovou pokrývku.
První Newtonův zákon nám říká, jestliže nepůsobí vnější síla na těleso, tak je v klidu nebo se pohybuje rovnoměrně přímočarým pohybem. Druhý Newtonův zákon pak svazuje sílu působící na těleso se zrychlením (přesněji změnou hybnosti).
Představte si sníh, co leží na svahu o konstantním sklonu, bez terénních překážek, svah je tedy homogenní. Jestliže se na svahu nikdo nepohybuje , pak na sníh působí jen tíhová síla země (zanedbejme silové působení větru, slapové síly apod.). Pak se lavina může uvolnit jen vlivem působení tíhové síly. Samozřejmě závisí na vnitřním napětí sněhu a řadě dalších faktorů. Tyto “vnitřní” faktory se typicky vyvíjí v průběhu určité doby v závislosti na počasí a podmínkách, jež panují v oblasti. Jakmile dojde k porušení sněhové vrstvy nebo k nějaké nestabilitě, tak se může uvolnit lavina. Na masu sněhu působí tíhová síla, a tudíž se může (kvůli druhému Newtonovu zákonu) pohybovat směrem do údolí.
Dodatečné působení člověka nebo zvířete
Když se po svahu pohybuje lyžař, pěší, nebo i zvíře, tak na svah působí dodatečnou silou, jak je uvedeno výše. A tudíž je vyšší pravděpodobnost, že se může uvolnit lavina.
Fyzikální předpoklady pro sněhovou lavinu
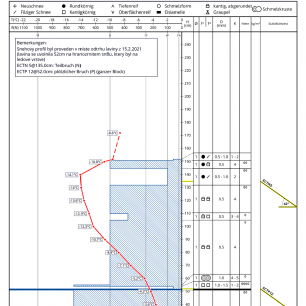
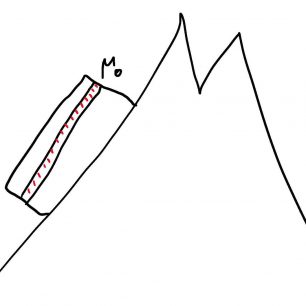
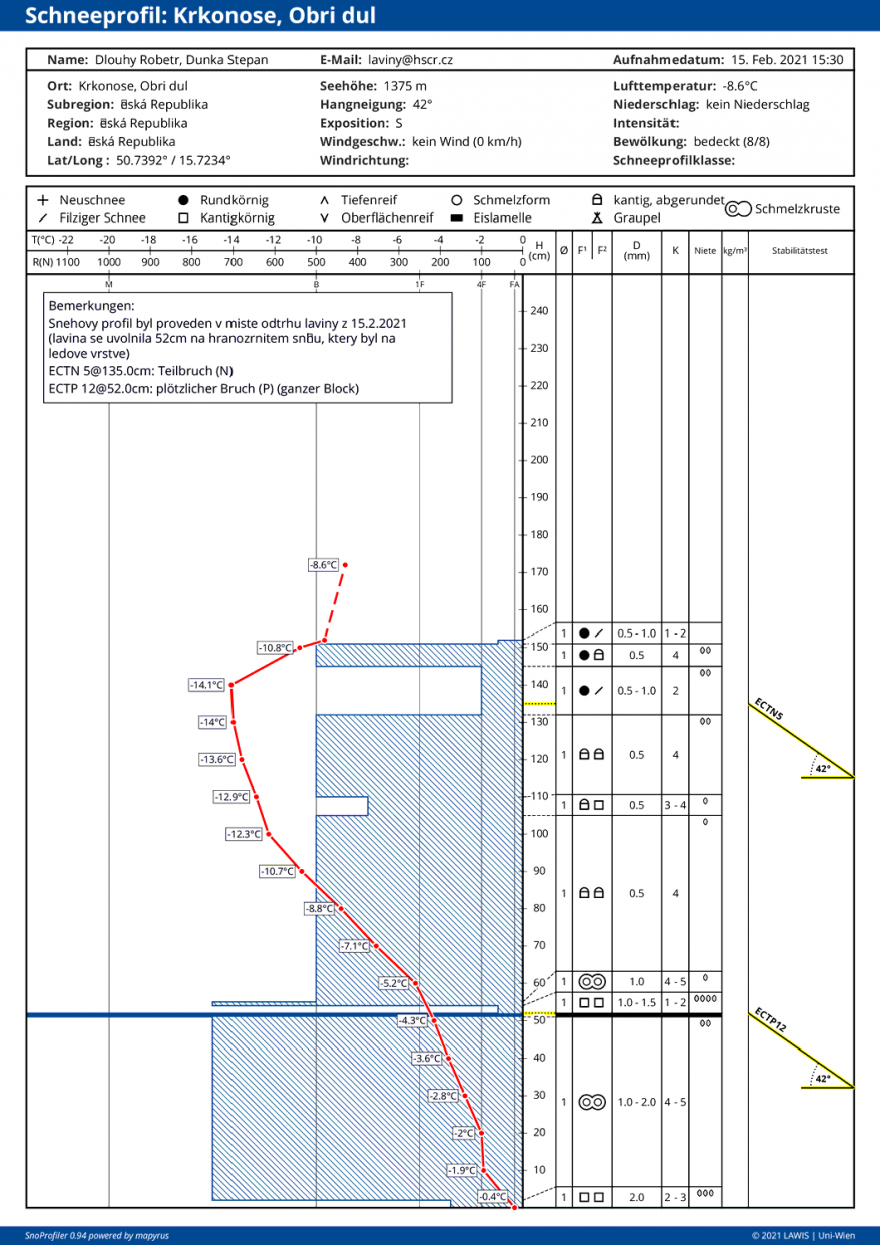
Sněhová pokrývka je většinou rozvrstvena do jednotlivých vrstev (viz obr. 1) s různou konzistencí sněhu (sníh má různou hustotu, tvrdost, skládá se z jiných částic…). Ve své práci se věnuji právě tomuto modelu – sníh je rozvrstven do různých vrstev. Pro zjednodušení následujících úvahu beru v potaz jen svah neměnného sklonu bez překážek a terénních nerovností. Předpokládám, že mezi jednotlivými vrstvami sněhu je určitý součinitel tření. Co to znamená?
Představte si kvádr položený na stole. Jestliže do něho tlačíte, tak se pohybuje. Pak do něho přestanete tlačit a on se po chvíli zastaví. Z fyzikálního hlediska na něj začnete působit silou, tudíž ho uvedete do pohybu. Když na něj přestanete působit silou – podle prvního Newtonova zákona by se měl pohybovat rovnoměrným přímočarým pohybem. On se ale zastaví – pohybuje se se zrychlením (“zpomalením” – vektor zrychlení míří proti směru pohybu).
Co to znamená? Podle druhého Newtonova zákona na něj musí působit síla. A je to síla třecí, jejíž velikost závisí právě na součiniteli smykového tření mezi kvádrem a stolem. Zde jsem použil pojem součinitel smykového tření a předtím jen součinitel tření. Mezi těmito pojmy je mírný rozdíl. Počítají se s nimi stejně, ale jestliže se těleso pohybuje po podložce, tak je tření smykové a většinou je součinitel smykového tření menší než součinitel tření, který působí na těleso v klidu. Jinak řečeno, chcete-li uvést těleso na podložce do pohybu musíte překonat třecí sílu (související se statickým součinitelem tření) a jestliže překonáte tuto sílu, těleso se začne pohybovat a proti pohybu působí síla určená součinitelem smykového tření.
Statický součinitel tření mezi sněhovými vrstvami
A to samé platí pro sníh na svahu. Sníh je běžně rozvrstven do vrstev a mezi každými dvěma vrstvami (a sněhem a podložím) je určitý statický součinitel tření. Nás zajímá právě ten nejmenší součinitel (kritické rozhraní).
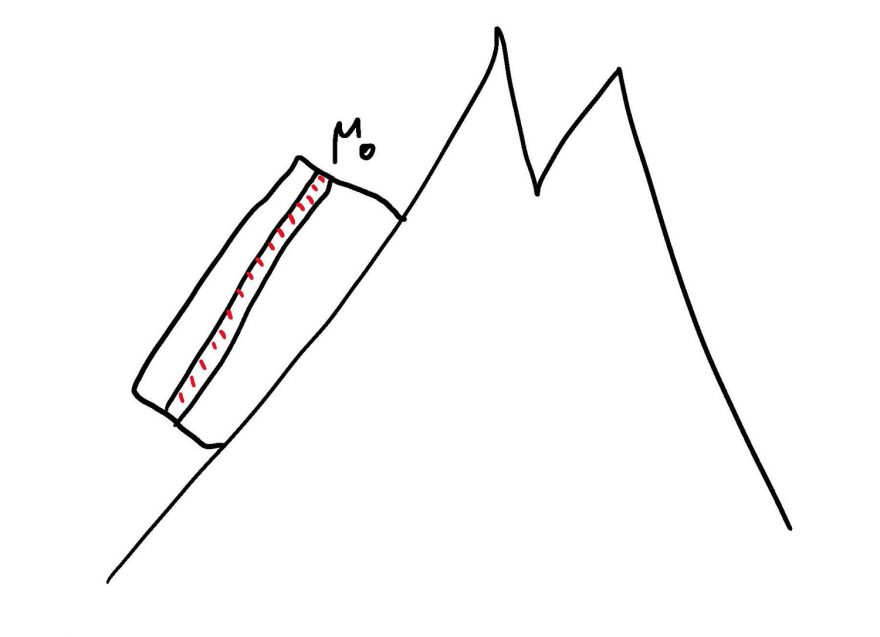
Nyní uvažujme, že se na svahu nepohybuje lyžař ani nic jiného. Na sníh působí tíhová síla. A jestliže tato síla překoná třecí sílu (na onom kritické rozhraní), tak se může uvolnit samovolná lavina. Tíhová síla je konstantní (neuvažujme zemětřesení), tak závisí na časovém vývoji součinitele (vlivem počasí apod.). Ten se může vyvíjet v závislosti na změnách vnitřní struktury sněhu.
Ke stažení: Teoretické odvození (pdf)
Pohybující se lyžař nebo snowboardista
Nyní se budu věnovat pohybujícímu se lyžaři (snowboardistovi). Nejsou uvažováni lidé pohybující se pěšky nebo na sněžnicích, a ani skialpinisté stoupající do kopce na tuleních pásech. To proto, že tam působí síly trochu jinak. V těchto případech je daleko větší lokální zatížení svahu a lavina se může uvolnit vlivem narušení nestabilní vrstvy přímo, mechanicky, tak, že se např. pěší propadne přes tuto vrstvu.
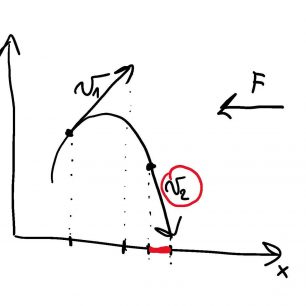
Uvažujme tedy lyžaře jedoucího dolu po svahu. Lyžař neustále mění svou rychlost, neboť dělá oblouky (pokud jede šusem dolů, tak také mění rychlost, viz dále). Jeho měnící se rychlost znamená, že se mění vektor rychlosti – velikost rychlosti se nutně nemusí měnit. Ovšem, jak je známo z kinematiky, tak zrychlení je časová změna rychlosti (přesněji derivace rychlosti). Jelikož se rychlost mění, tak se lyžař pohybuje se zrychlením. Poté dle druhého Newtonova zákona na lyžaře působí síla. A podle třetího Newtonova zákona působí také lyžař na svah silou stejně velkou, ale opačnou. Tudíž jestliže lyžař zabrzdí, tak na něj svah působí silou mířící “do kopce” a lyžař působí na svah silou stejnou, ale směrem “z kopce”.
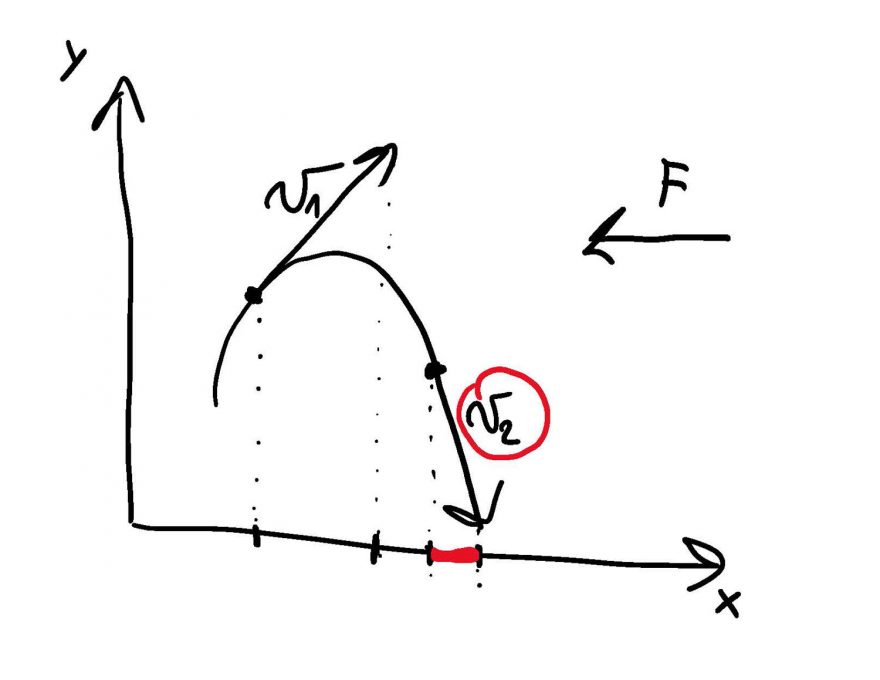
Pokud lyžař zatočí do oblouku, tak zpomalí ve směru dolů ze svahu. Velikost rychlosti zůstane stejná, jen se změní její orientace “šikmo ke svahu”, což znamená, že se rychlost ve směru dolů ze svahu zmenšila. Tudíž oblouk je také popsaný v předchozím modelu.
Uvažujme tedy, že lyžař působí na svah silou o velikosti úměrné časové změny své rychlosti. Poté je zjevně lehčí překonat klidovou třecí sílu na kritickém rozhraní. Ve své práci jsem došel k následující rovnici.
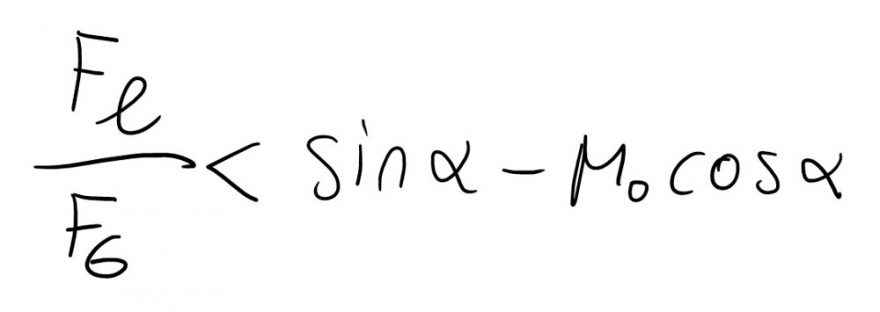
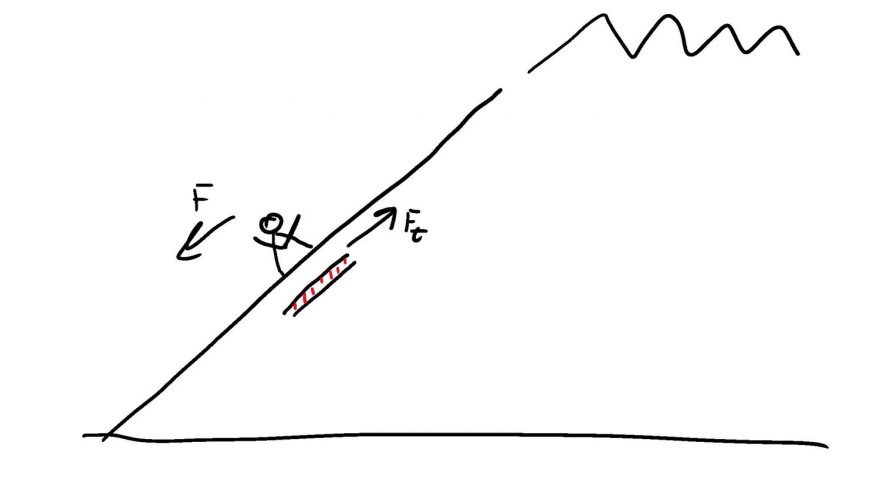
Výsledky působení lyžaře na zasněžený svah
Rovnice, která je napsaná výše lze upravit dále do tvaru:
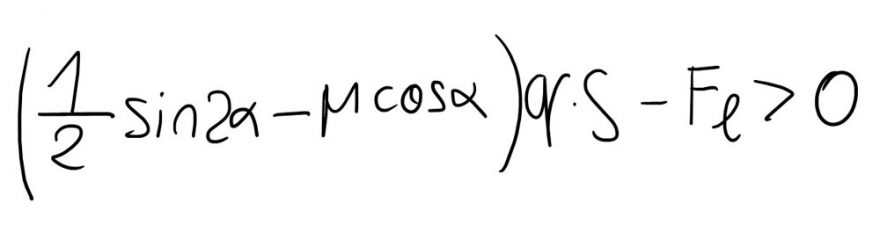
Výraz v závorce charakterizuje sklon svahu a vlastnosti kritické vrstvy, součin napětí a plochy má význam síly (tlakové) jež působí na rozhraní vlivem tíhy vrchních vrstev sněhu. Od této charakteristiky svahu se odečítá síla, jež působí lyžař na svah vlivem změny své rychlosti. Mohli bychom zadefinovat, že pravá strana je funkce L (svah, lyžař). Jinými slovy pravá strana je číslo závisející na svahu a lyžařovi “jak dovádí” a když je toto číslo větší než nula, pak se může uvolnit lavina. Samozřejmě je to třeba brát s velkou rezervou, jelikož jsme přijali řadu zjednodušujících faktorů a situace je v reálu daleko složitější. Což ovšem neubírá nic na faktu, že tento fyzikální model bude určitě s jistou přesností fungovat.
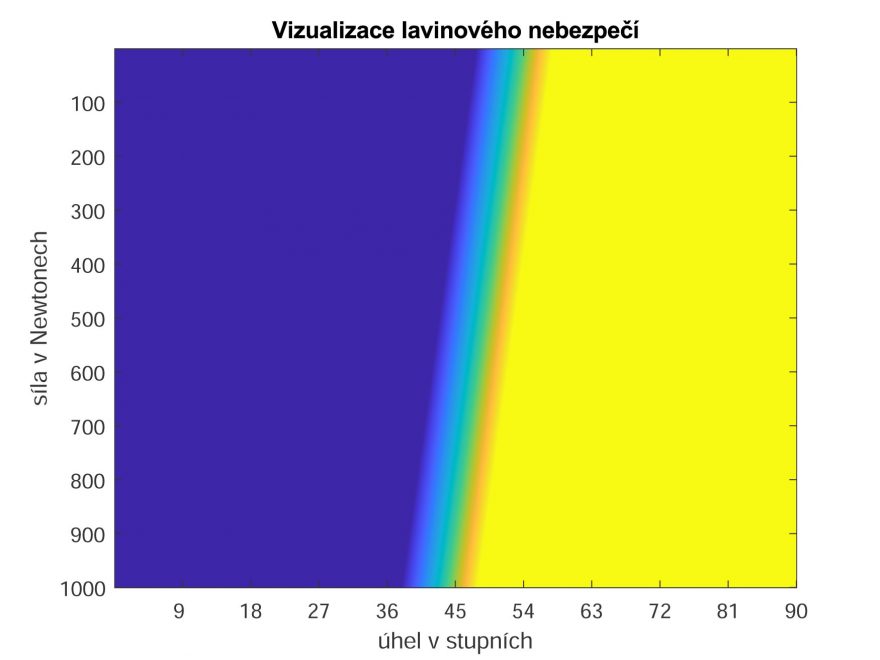
Tuto rovnici jsem se snažil vizualizovat a vymyslel jsem to následujícím způsobem. Uvažujme ono číslo L = L (lyžař, svah). Přiřaďme hodnotě 0 (a menší) modrou barvu a vyšším hodnotám jinou barvu (závisí na velikosti čísla). Jestliže takovýto graf vykreslíme, získáme například
Z obrázku je vidět, bude-li osmdesáti kilový lyžař brzdit se zrychlením 1m/s2, tak může lavinu uvolnit za výše stanovených podmínek od 45°. Naopak lze vidět, že pokud se lyžař bude pohybovat na svazích pod cca 36 °, tak mu víceméně hrozí jen malé nebezpečí. Ovšem na svazích nad 45° již hrozí uvolnění lavin i při nulové dodatečné síle, tj. samovolných lavin.
Vykresleme graf i pro jiné parametry
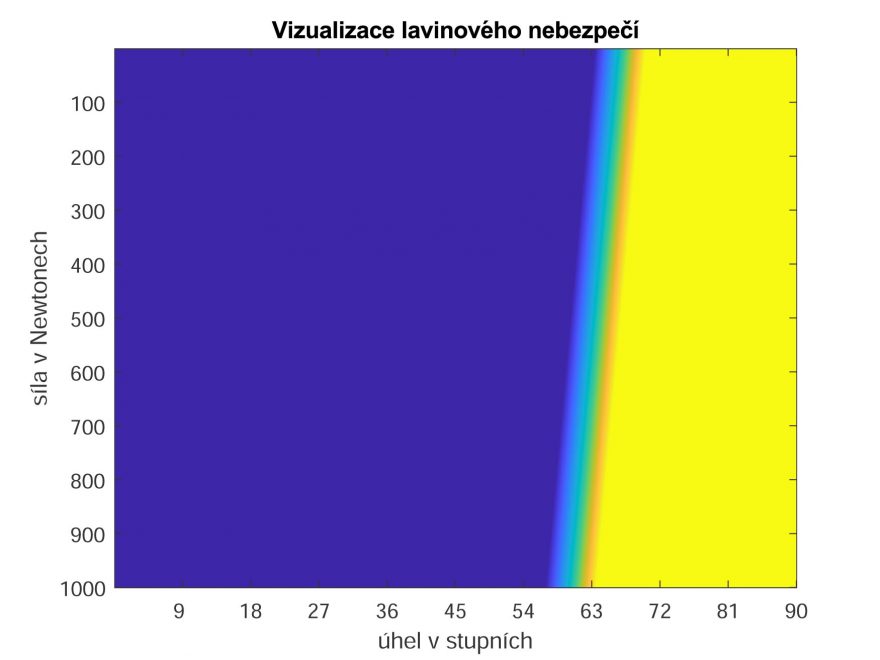
Z obrázku 8 lze nahlédnout, že zvýšení součinitele z hodnoty 1.1 na 2 posunulo hranici samovolných lavin na svahy nad 63° a bezpečné jsou svahy pod cca 54°. Z tohoto plyne, že tento fyzikální model je extrémně citlivý na změnu parametrů a těch parametrů je řada. Pro zajímavost ještě uvedu graf pro součinitel tření roven 0.7
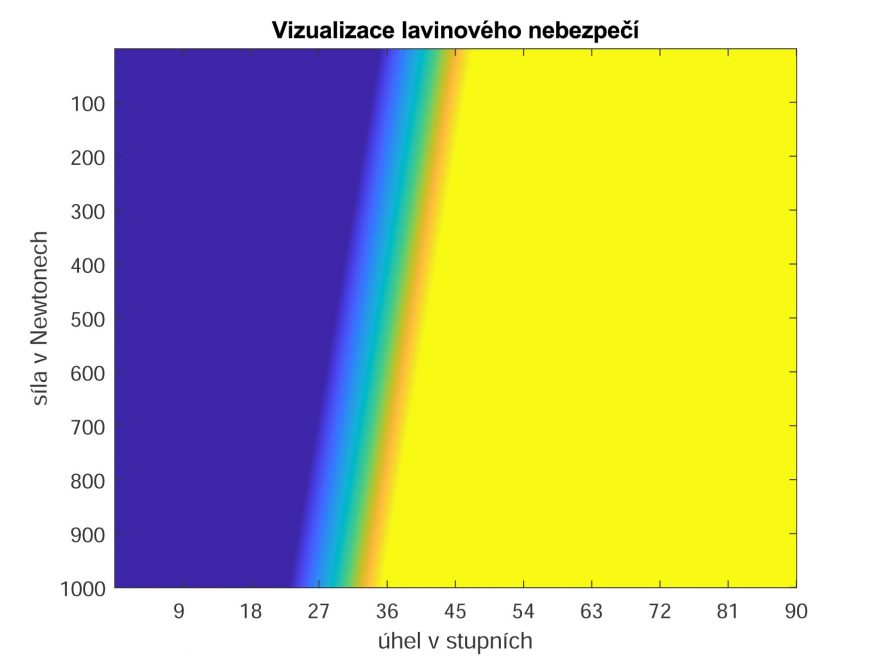
Z obrázku 9 můžeme vidět, že riziko samovolných lavin se posunulo na hranici 34° což již odpovídá velice zrádné situaci v oblasti.
Shrnutí zjednodušeného náhledu na působení lyžaře na zasněžený svah
Na závěr tohoto článku bych rád poznamenal, že i na základě velice zjednodušených předpokladů vede tato problematika na poměrně složitě řešitelnou úlohu s řadou vstupních parametrů, a řešení úlohy je navíc velice citlivé na volbu těchto parametrů. Na světě se této problematice věnují řady výzkumných týmů, a i tak je hlubší pochopení vzniku lavin zatím velice vzdálené. Proto nám nezbývá nic jiného, než se spoléhat na svou intuici a zkušenosti a řídit se pravidlem, když se mi to nezdá, tak tam nechodit.